4th Intern. Conf. on Seimic Zonation (August 26-29, 1991, Stanford, USA)

* Research Assistant, Dept. of Architecture, Waseda University, Ohkubo 3-4-1, Shinjuku-ku, Tokyo 169, Japan
** Professor, Dept. of Architecture, Waseda University, Ohkubo 3-4-1, Shinjuku-ku, Tokyo 169, Japan

ABSTRACT

To investigate the reason why surface waves excited in sedimentary basins are usually dominant at longer-periods, while body waves amplified in the basins are not, we conduct body and surface waves analyses using BEM and the analytical method for Love wave (Hisada et al. 1991), and obtain the following conclusions:
1) Shorter-period components of the surface waves are much more largely attenuated than those of the body waves, because the former waves travel mainly in low-Q (highly attenuated) basin sediments, while the latter does in high-Q bottom bedrock;
2) In comparison with the amplification factor due to the body waves, the factor due to the surface waves (Love waves in this study) has small amplitudes at shorter periods, that is, the fundamental mode of the surface waves is more efficiently excited in basins than the higher-modes.

INTRODUCTION

Surface waves observed in sedimentary basins or alluvial valleys are usually dominant at longer-periods, while body waves are at shorter-periods. As a typical example, we show strong ground motion records obtained in and around the Los Angeles basin during the 02/28/1990 Upland earthquake in Figure 1 and Figure 2. In the Figure 1, (a) is the geological map of the LA basin and vicinity, and locations of the epicenter and observational stations (CIT: Kresge Laboratory of Caltech, USC: University of Southern California), (b) is the geological cross sections from the hypocenter to CIT and USC, and Figure 2 is the broad-band velocity records at CIT and USC. From comparison between the records at CIT and USC, we can see that soft sediments (mainly Quarternary and upper Tertiary sediments) of the LA basin generate largely local surface waves in the basin, and the surface waves (about 40-80 sec of the USC record) are dominant at long-periods, thile body waves (about 20-40 sec) are at short periods.
The importance of surface waves to strong ground motions has been pointed out by a lot of researchers since early 1970's (e.g. Shima 1970, Trifunac 1971, Anderson 1974, Herrman and Nulti 1975, Hanks 1975, Kudo 1978, Seo 1978). However, there are not many theoretical studies regarding the reason why the surface waves in basin structures are dominant at long-periods, while the body waves are not. For the surface waves, Drake (1980) considered an alluvial valley model using 2-D FEM, and reported that large amplification in the valley did not occur at periods shorter than a certain period, because damping of the surface waves was effective and the higher modes of the surface waves did not have large amplitude.
In this study, we deal with amplification and propagation of both surface and body waves in sedimentary basins. In particular, we focus our attention on: (1) influence of damping (quality factor, Q) on both kinds of waves; (2) the difference of spectral shapes of the amplification factors due to both waves. Since Horike (1987) and Hisada et al. (1988) investigated the influence of Q on SH-body waves and Love waves in sedimentary basins, we first consider P, SV-body and Rayleigh waves using BEM (Boundary Element Method). Next we calculate the amplification factors due to SH-body waves (Haskell 1960) and Love waves (Hisada et al. 1990) using actual data of sediment layers in the Kanto and the Los Angeles basins, and investigate the difference of spectral shape between both kinds of amplification factors.

EFFECTS OF Q ON P, SV AND RAYLEIGH WAVES IN SEDIMENTARY BASINS

We first investigate the effect of Q on body waves (P and SV waves) and Rayleigh waves excited in sedimentary basins. Figure 2 (a) shows the sedimentary basin and source models used here, and (b) is seismic waves on the basin computed by 2-D BEM with a dislocation source (Hisada et al. 1988). In the figure, solid lines indicate the computed waves considering Q and dotted lines without Q. We can see from both waves that the body waves are less attenuated by Q, while the Rayleigh waves are largely attenuated. This is because the former waves mainly travel in high-Q bedrock, while the latter waves do in low-Q basin sediments. This result agrees with the one for SH-body and Love waves by Horike (1987) and Hisada et al.(1988).

AMPLIFICATION FACTOR DUE TO BODY AND LOVE WAVES IN THE KANTO AND THE LOS ANGELES BASINS

As the amplification factor due to body waves using the Haskell(s method is well-known, we first mention briefly the analytical method for Love waves generated in multilayered sedimentary basin (Hisada et al., 1991), second define the amplification factor due to the Love waves using this method (Hisada et al., 1990), and last apply this factor to the Kanto and Los Angeles basins. We have already confirmed that this method gives exact solutions, with the advantage of much less computing time and memory than BEM (Hisada et al., 1991).

Analytical method for Love waves excited in multi-layered basin
As shown in Figure 3, the medium for this method is composed of two 2-D elastic quarter-spaces welded along the vertical interface X=X'; one quarter-space is homogeneous (Domain 1, bedrock) and the other is layered with flat interfaces (Domain 2, basin sediments and bottom bedrock). The incident wave is a plane SH-wave whose amplitude varies with depth, and travel horizontally in Domain 1. The reflected wave from the vertical interface is also a plane SH-wave, neglecting the contribution of the waves diffracted at the corners formed by each layer and the vertical interface. The waves transmitted into Domain 2 are superposed by Love wave modes (normal modes), neglecting the body wave contribution excited at the vertical interface. Defining the time-dependent factor as e^iƒÖt, the analytical expression of the Love wave V₂ at ƒÌ₁ on the free surface in Domain 2 is given as follows:

...............(1)

where M is the maximum mode of Love wave for the considered frequency ą, N is the total number of layers including the bottom bedrock, N_b is sub-divided layers in the bedrock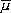, _2j is the rigidity of the jth layer, 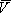_1j^I is the amplitude of the incident waves in the jth layer along the vertical interface, and k^m is the wave number of mth Love mode. The analytical expressions of the transmission coefficient 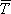_j^m and ĢA_Lj^m are to be referred Hisada et al.(1991).

Amplification factor due to Love waves
We define here an amplification factor due to the Love waves excited in sedimentary basins using the above method. The factor AF_L^m on the free surface due to mth Love mode is derived from the absolute value of mth mode of equation (1), assuming that the incident wave 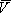_1j^I as the plane SH-wave with unit amplitude, as follows:

...............(2)

Note that this value is independent of the distance from the vertical boundary (the basin edge). This factor is physically equivalent to the displacement of the mth Love mode at a point on the free-surface of Domain 2, which is generated by the plane SH-wave with unit amplitude traveling horizontally in Domain 1.

Amplification factors due to body and Love waves in the Kanto and the LA basins
We consider here two sedimentary layer models as shown in Table 1: the KNT (the Kanto sedimentary basin, Japan) model and the LAB (the LA basin) model. The values of material properties and thickness of each layer in the KNT model are directly measured using the deep bore-hole at Shimofusa (Ohta et al.1980), and those of the LAB model are quoted from the data by Wald et al.(1987).

TABLE 1. The Kanto and Los Angeles basin models

(a) The Kanto sedimentary basin (KNT)

layer	ƒÏ (g/cm3)	VS (km/s)	thk (km)	dpt (km)
1	2.0	0.45	0.272	-
2	2.1	0.70	0.497	0.272
3	2.2	0.90	0.345	0.769
4	2.5	1.17	0.309	1.114
5	2.7	2.54	0.800	1.423
6	2.7	3.00	-	2.223

(b) The Los Angeles basin (LAB)

layer	ƒÏ (g/cm3)	VS (km/s)	thk (km)	dpt (km)
1	1.7	0.50	0.20	-
2	1.7	0.60	0.30	0.20
3	1.8	0.90	0.20	0.50
4	1.8	1.20	0.20	0.70
5	1.8	1.50	0.30	0.90
6	1.9	1.60	0.50	1.20
7	2.0	1.70	0.30	1.70
8	2.1	2.10	0.30	2.00
9	2.1	2.20	0.70	2.30
10	2.2	2.50	0.20	3.00
11	2.3	2.70	0.70	3.20
12	2.4	2.80	0.30	3.90
13	2.5	3.00	-	4.20

As shown in Figure 4, the amplification factors due to Love wave are plotted by solid lines and those due to SH-body waves are dotted lines. The latter factors are computed by the Haskell's matrix method (Haskell 1960) under vertical incidence of SH-wave with unit amplitude. Although two kinds of the amplification factors show very similar spectral shapes, those of Love wave are slightly small, in particular for higher frequencies. In other words, higher Love modes tend to become smaller than the fundamental mode. This is probably because the particle motion of the fundamental Love mode is in phase with that of the incident wave (plane SH-wave horizontally propagating) along all depth, while those of the higher modes are out of phase at certain depth (Hisada et al., 1990).
Although we consider here simple basin models with rectangular edges and flat layers, we probably obtain similar results for more complicated and realistic basin models. Because long wave-lengths of the fundamental mode of surface waves are less influenced by the complicated structures than those of the higher modes. In fact, Drake (1980) reported that higher modes of surface waves in a realistic basin model have much less amplitude than the fundamental mode.

CONCLUSION

We have investigated reasons why the surface wave excited in sedimentary basins are dominant at longer-periods, while the body waves amplified in the basins are not, using the boundary element method (BEM) and the analytical method for Love wave by Hisada et al.(1990, 1991). The results are summarized as follows;
1) Since the surface waves travel mainly in low-Q (highly attenuated) basin sediments, their shorter-period components are largely attenuated. On the contrary, the body waves travel mainly in high-Q bedrock and are little attenuated.
2) In comparison with the amplification factor due to the body waves, the factor due to the surface waves (Love waves in this study) has small amplitudes at shorter periods, that is, the fundamental mode of the surface waves is more efficiently excited iin the basin than the higher-modes.

ACKNOWLEDGMENTS

We are grateful to T.-L. Teng of University of Southern California for help to obtain the digital records of the 1990 Upland earthquake.