ここで、関東平野のやや長周期地震動に関する既往の研究を振り返る。やや長周期の地震動が、関東平野の厚い堆積層によりしばしば増幅されることは、地震動観測 4)や関東地震の記録の復元 5)などを通してかねてから指摘されていた。岡田ら 6)はやや長周期対行きにおける全国各地の'ゆれやすさ'を統計的に求め、東京における値が全国平均の２倍程になること、また、これが深い地盤構造の影響によるものであることを示した。工藤 7)は、関東平野の平均化された地下構造を表面波の分散をもとに定め、これに平行層仮定の正規モード理論を適用することにより、東京での長周期地震動主要部をよく再現できることを示した。ただし、伊豆半島沖地震における主要動後続の波動は、東京と伊豆半島の平行層地盤を鉛直境界で接続したモデルを用いても十分説明されなかった 8)。ほぼ同じ頃から、人工地震波や実地震波の走時解析などによる関東平野の基盤構造に関する精力的な調査・研究が始められ 9),10)、現在では関東平野全域にわたるVs≒3.0km/sec層上面の構造がかなり明らかにされている 11)。その結果、関東平野は典型的な盆地状構造をしていること、すなわち、基盤は平野中央部で深さ2〜3kmとなり、平野外周部で路頭していることが示された。山中ら 12)は、関東平野西部の２次元地盤モデルを扱った表面波入力による応答解析を行い、現実的な地盤モデルを扱うことにより平野内各地点での実地震動の性状をよく説明できることを示した。
以上の事柄などを背景に、地盤および震源情報が与えられた際の、関東平野内部における地震動の定量評価の可能性を調べることを目的とし、２次元盆地状地盤モデルと、公表された断層パラメタを使用して、関東平野のやや長周期波動のシミュレーションを行う。対象とする地震として、すでに断層パラメタが知られており、関東平野内でやや長周期波動が卓越した1980年伊豆半島東方沖地震、1974年伊豆半島沖地震、1930年北伊豆地震を扱う。また、震源特性、伝播特性、増幅特性を考慮できる大規模な波動場のシミュレーション法として、離散要素数が少なく、無限遠境界処理の容易な境界要素法(BEM)に、断層震源モデルを組み込んだ手法を用いる。
本報では、はじめに断層パラメタを用いた２次元の解析手法を示す。次に、対象となる地盤、震源のモデル化について述べ、モデルに対する本解析手法の適用性を調べる。シミュレーション実行後、計算波形と観測波形との比較を通し、1) ２次元地盤モデルを用いた波動解析の妥当性、問題点、2) やや長周期帯域で特に問題となる表面波の性状とその生成位置、震源の違いが平野内の波動に与える影響、などに関して検討する。
kinematicな断層震源モデルを含んだ境界要素法(BEM)の定式は久田ら 2)によって示されており、食い違い断層を含んだ２次元波動場の境界積分方程式は、周波数領域で次のように表すことができる。
ここで、ξは境界上の観測点、ζはソース点位置を表す２次元ベクトルである。また、V、Pは境界における面外方向の変位、表面力を表し、V2*、P2*は２次元場におけるグリーン関数と、その応力表示である。Cは境界の形状によって定まる係数、Γ0、Γ1は、それぞれ外部境界、内部境界（食い違い断層）を示す。[V]は断層面における食い違い変位量である。...............(1)
式(1)右辺が断層からの入力項となり、ここに３次元場で定義されている断層パラメタを用いるためには、３次元断層の２次元波動場への近似的な変換をする必要がある。このような変換に関してHelmbergerらによる手法 13)などがあるが、ここでは、３次元断層を放射特性を有する線震源の形に近似的に置き換え、２次元境界要素法に組み込むことにより、断層パラメタを直接扱えるようにする。ただしSH波、Love波を対象とし、以下の仮定を設ける。
1) 断層は堆積盆地の遠方に位置し、断層の３次元的広がりが波動に与える影響は無視できるものとする。
2) 堆積盆地の３次元的形状による面外からの回り込み波動の影響は無視できるものとする。
図−１に概念図を示す。座標は図に示したような３次元直交座標系を考え、このうち断層代表点と堆積層内の波形出力点を含むX-Z面を２次元場として扱う。図中、A点は断層上の代表点、B点は堆積盆地端部の点である。このとき、３次元断層と同じ波動をB点に与える２次元の線震源（A点）を求め、この線震源を用いて２次元波動場の定式を行うものとする。まず、断層パラメタを用いて、均質な３次元全無限体内のB点における、３次元食い違い断層からの波動を求める。すなわち、
ここで、...............(2)
、
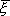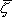は３次元場の位置ベクトル、P3*は全無限３次元場におけるグリーン関数の応力表示、[U]は３次元断層面における食い違い変位量を表すベクトルである。次に２次元場において、断層面の食い違い変位が一様に[VF]である２次元断層を考える。このとき、３次元断層面の法線をX-Z面へ射影することにより２次元断層面の法線方向を求め、震源の放射特性を考慮できるようにする。２次元断層のX-Z面における幅がAB間の距離に比べて十分小さいとき、断層は線震源として扱うことができ、２次元全無限体内のB点における断層からの波動は、
となる。...............(3)
B点で３次元断層による波動と同じ結果を与える２次元断層を、疑似３次元断層とみなし、式(2)、(3)を用いて、式(1)を次のように書き換える。
式(4)の積分区間を離散化し、図−１における堆積盆地部との境界条件を満足させることにより堆積盆地上での波動を求めることができる。また、時間領域における結果は、高速フーリエ変換を用いて求める。...............(4)
関東平野は周囲を露頭した新第三紀系や先新第三紀系の地盤に囲まれ、堆積盆地構造を成している（図−２参照）。平野内部における基盤（Vs3.0km/sec）深度は、主に首都圏基盤構造研究グループによる人工地震実験データの蓄積、解析などにより、３次元的にほぼ解明されている 11)。平野内部の堆積層に関しては、やや長周期帯域の地震動を対象とした場合、表層付近のごく薄い層は無視できると考えられ、平野中央部で、上総層群（Vs≒0.7km/sec）、新第三紀系の三浦層群・葉山層群（Vs≒1.5km/sec）は基盤上部にVp=4.8km/sec層が存在することが報告されているが、関東平野中央部でのLove波（卓越周期約8〜10sec）に最も影響を与える層が0.7km/secの層であることが解析的には知られていること 12)から、本研究では、最上層のVsを0.7km/sec、基盤層を3.0km/sec、中間層を均一に1.5km/secと考えて３層でモデル化する（図−３参照）。各層境界の形状は文献 11)に示された等深図により定めた。現実には震源から、観測点までの方位は各地震ごとにややずれ（東京では方位角にして30°程度）があるが、ここでは、震源から観測点までの地盤断面形状はどの地震の場合も等しいと仮定している。また、相模湾内の地下構造は現時点で明確ではないため、震源域から盆地端部までの堆積層、トラフによる不連続面の存在は考慮せず、1.5km/secの層を相模湾内部で傾斜状に立ち上げた。震源方向のずれ、相模湾内部の地下構造の影響に関しては、後ほど考察を行う。さらに、ここでは堆積盆地への入射角が大きな浅い震源を扱うため、震源とは反対方向の盆地端部からの回折波、反射波による影響は無視できると考え、盆地内観測点から震源方向にかけての地下構造のみをモデル化する。したがって、図−３に示されていない堆積盆地右半分の境界は、シミュレーションに際して積分区間に含まれない。盆地右半分を扱わないことに関する検討は文献 2)を参照されたい。
3.2 解析対象とする地震・断層モデル
1980年伊豆半島東方沖地震（M=6.7, H=10km）、1974年伊豆半島沖地震（M=6.9, H=10km）、および1930年北伊豆地震（M=7.3, H=0km）を扱う。静的断層パラメタとして、断層長さ(L)、幅(W)、走行方向(θ)、傾き(δ)、食い違い方向(λ)、地震モーメント(MO)、また動的なパラメタとして、立ち上がり時間(τ)、破壊伝播速度(Vτ)を扱う。伊豆半島東方沖地震の静的・動的断層パラメタは入倉 14)による値を用いた。また伊豆半島沖地震、北伊豆地震の静的断層パラメタに関しては、阿部 15)、Chinnery 16)による値をそれぞれ用い、明記されていない動的パラメタに関しては、τ=1.5sec、Vτ=2.5km/secと経験的な値 17)を使用した（表−１）。なお、食い違いの時間変化は傾斜関数により評価し、食い違い量、破壊伝播速度が断層全体にわたって一様なHaskellタイプの震源であると仮定した。
計算波動との比較に用いる堆積盆地内のやや長周期の観測波形として、東京、横浜における変位形記録を使用する。東京における観測記録は、東京大学内の大森式長周期地震計（伊豆半島沖地震、北伊豆地震）、大手町の気象庁一倍強震計（伊豆半島東方沖地震）によるもの、また横浜における観測波形は、横浜地方気象台の気象庁一倍強震計（伊豆半島東方沖地震、伊豆半島沖地震）によるものである。大森式長周期地震計の変位記録は、田中ら 18)により数値化されたデータをtransverse成分に変換して使用した。一倍強震計の変位記録は、ディジタイザーにより数値化し、計器補正、バンドパスフィルター（周期2.5〜12sec）処理等の後、transverse成分に変換している。また震源付近の観測記録として、SMAC-Bによる川奈（伊豆半島東方沖地震）でのディジタル加速度記録 19)を用いた。
| 伊豆半島東方沖地震(1980) | 伊豆半島沖地震(1974) | 北伊豆地震(1930) | |
| L (km) | 15.0 | 18.0 | 24.0 |
| W (km) | 7.5 | 8.0 | 12.0 |
| θ (deg) | N165E | N307E | N15E |
| δ (deg) | 90 | 80 | 90 |
| λ (deg) | 0 | 197 | 0 |
| M0 (dyne*cm) | 7.0×1025 | 5.9×1025 | 2.7×1026 |
| τ (sec) | 1.0 | 1.5 | 1.5 |
| Vr (km/sec) | 3.0 | 2.5 | 2.5 |
| 破壊開始点 | 断層面下端 中点 |
断層面下端 中点 |
断層面北側 端部 |
3.3 解析手法で適用に関する妥当性の確認
２章で示したシミュレーション手法に関して、本題で扱う関東平野・断層モデルに対する適用性を検討する。本手法では堆積層端部の点（図−１、B点）で３次元解と等しい解が得られるよう定式を行っているため、波形出力点がBから離れるにつれ、本手法による解と３次元解との差異が大きくなる。点震源を扱い、基盤層と堆積盆地層の物性を等しくした見かけの半無限地盤モデルを用いた場合、この差異は単純に３次元、２次元の幾何減衰の違いとして評価できる。すなわち震源から盆地端部までの距離、震源から波形出力点までの距離をそれぞれR1、R2とするならば、本手法による波動の振幅は３次元解の振幅を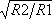
倍したものとして与えられる。ところが、断層面が広がりを持ち、さらに断層上での破壊伝播の影響が無視できない場合、本手法による解は、３次元解と比較して波動の振幅のみならず形状も変化することが考えられる。ここではそれらの影響を調べるため、３次元的な広がりを持つ断層を扱い、半無限体地盤モデル内において、本手法による解と３次元解との比較を時間領域で行う。断層パラメタとして伊豆半島東方沖地震の値を用い、２次元震源スペクトルを求める際に必要なB点の位置は、3.1に示した関東平野モデルと震源との位置関係により定める。
図−４に、堆積盆地上における本手法の解（２次元解）と３次元解との比較を示す。ただし、３次元モデルによる解は、全無限体内における結果に2を乗じたものである。図より、３次元解と比較した場合、盆地端部から離れるにつれて、振幅は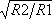倍よりやや大きくなり、初動到達時間が遅れ、初動到達から主要動（図中の矢印）到達までの部分の精度が悪くなる傾向が認められる。これは、本手法ではB点のX-Z面外波動を、すべてSH波とみなし線震源スペクトルを決定しているためである。実際には断層面の拡大に伴い、X-Z面での面外波動にもP波、SV波が含まれるようになるため、SH波のみを考慮した線震源によって、面外波動を厳密に再現することは困難となる。特に、伝播速度の異なるP波部分（初動部分）は評価できない。ただし、P波、SV波の寄与はSH波と比較して小さく、主要動の形状はほぼ再現されていることから、中規模の震源がここで扱ったような震央距離に位置する場合にも、P波初動部分が再現されないこと、主要動の振幅が３次元解と異なることなどに留意すれば、本手法が適用可能であることが示された。
3.4 シミュレーション結果
(A) 1978年伊豆半島東方沖地震のシミュレーション
初めにここで扱う断層パラメタの妥当性を確認するために、断層震源に近い（Δ=12km）川奈における計算波形と観測波形の比較を行う。計算波形は、全無限３次元場における食い違い断層震源モデルにより計算された波動に、表層地盤での重複反射による振幅率を乗じて求めたものである。計算に用いた地盤表層のモデルは、工藤 20)を参考に定めた（表−２）。図−５に計算波形と観測波形の比較を示す。計算では振幅の小さな後続波動が再現されていないが、観測波形主要動部分のパルス的な形状、振幅はよく再現されている。したがって、やや長周期帯域を対象とした断層パラメタが十分な制度を持っているものと考える。
次に、盆地内部の横浜、東京の各観測点における計算波形と観測波形との比較を行う。計算は２章で示した手法により行い、対象とする周期は2.5sec以上とした。図−６に、盆地各部における計算波形と対応する観測点で記録された波動のtransverse成分を変位表示で示す。計算波形は、盆地端部から、盆地中央部に波動が伝播するにつれて、周期8〜10sec程度の波動が分散する様をよく示している。特に、基盤と堆積層との境界面がほぼ水平となる関東平野中央部において波動はより大きな分散を示すようになることが分かり、東京付近での移送速度がLove波基本モードの理論分散曲線状にプロットされること（図−７）から、これらの波動が基本モードのLove波であることが示される。観測波形と比較した場合、横浜での主要動の前半部分（継続時間約30sec）、東京での主要動部分（継続時間約60sec）の位相は良く対応づけられ、盆地内部の観測波形の主要動成分は、三浦半島付近から関東平野にかけて存在するVs≒0.7km/sec層内部で主に成長したLove波であることが分かる。また、２次元場計算における振幅の過大評価も3.3の結果に比べ小さく抑えられており、東京における振幅の増大は３割以内に収まっている。これは、主要動が、主に盆地内部で成長した２次的な表面波によって構成されているためと考えられる。ただし、横浜における主要動後半部は位相、振幅とも観測波形との対応がつかず、東京における後続波群も計算では再現されていない。
| 層 | Vs (km/sec) | ρ (t/m3) | Q | 層厚 (km) |
| 1 | 1.5 | 2.2 | 30 | 1.0 |
| 2 | 2.5 | 2.3 | 50 | 3.0 |
| 3 | 3.0 | 2.5 | 100 | ∞ |
(B) 1974年伊豆半島沖地震のシミュレーション
横浜、東京における計算波形と観測波形との比較を図−８に示す。図より、両地点での観測波形主要動部分（継続時間はそれぞれ約30sec、約60sec）の位相は、計算波形と良く対応し、主要動部分における計算波形の最大振幅は、観測波形に比べ横浜で２割、東京で４割程度増大していることが分かる。特に横浜での振幅、位相に関する両現性は、(A)の伊豆半島沖地震の例に比べ良い。ただし、(A)同様、後続波群は再現されていない。
(C) 1930年北伊豆地震のシミュレーション
東京における計算波形と観測波形の比較を図−９に示す。本地震は他の地震に比べ震源方向がやや異なるが、同一の地盤モデルで主要動に関しては(A)、(B)と同等の再現結果が得られた。本地震に関しても、観測記録に認められる後続波動が、計算では再現されていない。
3.5 考察
シミュレーションの結果、関東平野の２次元堆積盆地状地盤モデルを用いて、盆地内における主要動の位相を、振幅に関して２〜４割以内の誤差で再現できることが分かった。なお、計算波形における振幅の増幅は 3.3 に示した結果などからほぼ予測できる値である。これら計算波形、観測波形との比較、理論分散曲線との対応などから、堆積盆地中央部で観測される主要動は、主として Vs≒0.7km/sec 層内で成長したローカルな表面波であることが示された。また、震源特性の異なる３つの地震に関して、盆地内部（特に東京）における波動の位相がほぼ同様の性状を示すことなどから、盆地内部における周期8〜19secの主要動は、基本的に震源特性より、むしろ堆積盆地の不整形状による伝播特性や増幅特性を強く反映していることが確認できた。さらに震源方向のやや異なる地震の主要動が、同一の2次元地盤モデルでほぼ再現されたことより、やや長周期波動の主要動を対象にする場合、関東平野南西部はここで用いた盆地状地盤構造で扱うことができると考えられる。
ただし、いずれの地震のシミュレーションに関しても、主要動に続く後続波動は再現されなかった。その理由として次のような事柄が考えられる。
1) 震源から堆積盆地までの地盤構造が均一であると仮定している。
震源から関東平野に至る相模湾内の地下構造は、現在明確に決定されていないが、実際には相模湾内に堆積層が存在することが報告されている 21)。また、堆積盆地端部に近い横浜における観測記録の主要動後半部に、既にある程度分散した波群が見られ、盆地への入射波そのものに相模湾の堆積層の影響を受けた表面波が含まれている可能性が高い。したがって、後続波動を考える際、相模湾内における堆積層など不整形構造の存在を無視することはできないと考えられる。
2) 地盤構造を２次元でモデル化している。
現実の地盤構造は３次元であり、本研究で扱った２次元平面内を伝播する波動のみならず、面外から回り込む波動も存在する。単純な形状をした３次元モデルによる波動解析などからも、３次元盆地内では、２次元盆地内に比べ波動の継続時間が長くなる傾向があることが報告されている 22)。したがって、現実の複雑な３次元形状をもつ地盤では、回折波や反射波の影響はより大きくなり、盆地内部における波動の継続時間をさらに延長させるものと考えられる。
関東平野内におけるやや長周期地震動の後続波動に関してより詳細な情報を得るためには、以上の点に関しても調査、観測および解析をする必要がある。
1) 関東平野内におけるやや長周期主要動の位相を、食い違い断層震源モデルと２次元の盆地状地盤モデルによって、振幅に関して２〜４割以内の誤差で再現できた。したがってやや長周期波動の主要動を対象にする場合、平野南西部はここで用いた２次元盆地モデルで扱うことができる。ただし、観測波の主要動後続の波群は、ここで扱った２次元の盆地状地盤モデルでは再現できなかった。
2) 観測波形と計算波形また理論分散などとの比較により、関東平野内で観測されたやや長周期主要動は、主に堆積盆地内部 Vs≒0.7km/sec 層で励起されたローカルなLove波であることが分かった。また、関東平野中央部におけるやや長周期波動は、震源特性に比べ、堆積盆地構造による波動の伝播特性、増幅特性をより大きく反映していることが明らかにされた。