ガウス型関数 注:以下はベンチマークテストstep3,T31モデルの入力例である。 Number of Time Windows Interval Time (s) Slip Velocity Func.(Rectangular=0; Triangle=1; Exponetial=2; Gaussian=3; Nakamura & Miyatake =4) fmax (Hz; only for Nakamura & Miyatake) dtN (sec; dt fot only Nakamura & Miyatake) 1 0 3 1 1 Time Window Number 1st Half Rise Time (s) 2nd Half Rise Time (s) 1 0.2 0 Source Data Pattern (=1: Original (ex. grflt12s.f), =2: Time Window Matrix (Displacement: m), =3: Time Window Matrix (Seismic Moment: Nm) 2 1st Time Window Slip (m) Strike 1 1 30866008.34 Rake (deg) Strike 1 1 0 ガウス型関数： ガウス型関数を用いる場合、Slip Velocity Func.でGaussian=3を入力。下記の式より、σ=1st Half Rise Time (s)であり、 1st Half Rise Time (s)にて入力した値の 4 倍がモーメント・レートの時刻歴関数におけるピーク時刻に相当するよう設定されている。 （上記例では　0.2（s）　×　4　＝　0.8(s)) また、2nd Half Rise Time (s)には 0 を入力する モーメント・レートの時刻歴関数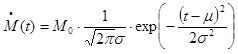は(1)式で与える（破壊開始時刻をt=0とする）。 ， σ=0.2(s), μ=4σ=0.8(s)　　　　　…(1-1) ここで，tは時刻(s)，σ，μは定数．μがピークの時刻に相当する．(1)式は裾野がゼロにならないので，便宜的にピークから-4σを破壊開始時刻とする（図1-3）．モーメントの時刻歴関数M(t)は(1)式の積分より、(2)式となる（図1-4）． ，　σ=0.2(s), μ=4σ=0.8(s)　　　　 　…(1-2) ここで，erf(x)は誤差関数であり，(3)式で表される． …(3) erfは初等関数で表せないが，Fortranでは組み込み関数erf( )がある．また近似式もある（数値解析手法（2010）の資料１参照）． 一方、 (1)式のフーリエ変換は次式になる（図1-5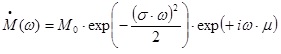）。 ， 　　　 　　　　 　　　…(1-3) ここで、i は虚数である。 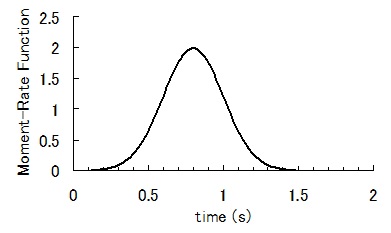　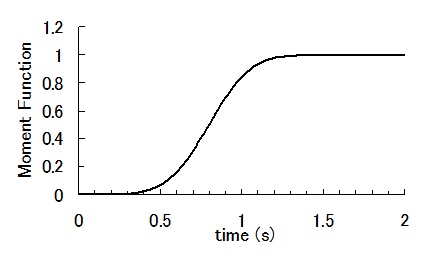　　　　　　　図1-3　モーメント・レートの時刻歴関数（Moで基準化）　　　　　　　　　　　　　　　　　図1-4　モーメントの時刻歴関数（Moで基準化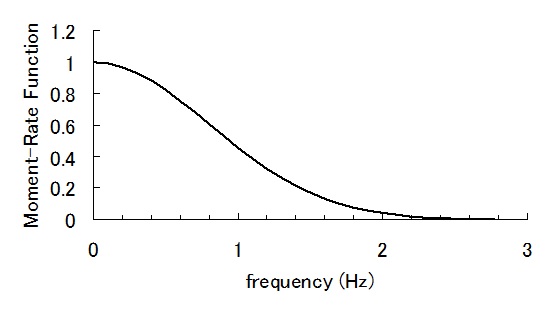） 　　　　　　　　　　　　　　　　　図1-5 モーメント・レート関数のフーリエ変換