波数積分データ（静的項） *** Data for Static Wavenumber Integration using Greenfield's Quadrature *** The first corner (om*k) on real axis (ex. 2.0) Initial Number of Intgegration Points for Adaptive Newton-Cotes Quadrature 2 16 The second corner (om*k) on imag. axis (ex. 10.0) Initial Number of Intgegration Points for Adaptive Newton-Cotes Quadrature 10 32 波数積分データ： ・グリーン関数の計算は、積分の効率化のために動的項と静的項に分けて行われる。 ここで、Tik は動的グリーン関数の応力テンソルであり、TikS はその静的項である。従って、上式の右辺第１項が動的項、第２項が静的項となる。 波数積分データ（静的項）： ・静的項の波数積分は積分路変換法（Greenfield法）によって行われる。まず波数kを区間kaで分割する。 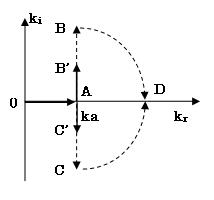上図　静的項の波数積分法 上のデータでは、ka×水平距離（r）に2.0とし、上式の第１項の波数積分としてNewton-Cotes積分を用い、その積分点数の初期値として１６点を用い、 精度が十分収束するまで積分点を増加させる。一方、第２項はベッセル関数をハンケル関数に変換し、 第１種、第２種のハンケル関数の積分路をコーシーの定理より、図４に示すように積分路を変換する。 第１種は虚数軸の上側、第２種は下側とすると、ハンケル関数は指数関数で速やかに収束する。上のデータでは打ち切りの波数×水平距離（r）に10.0を、 その積分点数の初期値として１６点を用いている。10.0で収束しないときは２倍の波数を用い、それでも収束しないときはまた２倍と次々に増加させ、 Newton-Cotes積分で精度が十分収束するまで行う。