| 中村・宮武関数 | |||||||||||||||||
注:以下はベンチマークテストstep4,T41モデルの入力例である。
中村・宮武関数: 中村・宮武関数を用いる場合、Slip Velocity Func.で Nakamura & Miyatake = 4 を入力。Rise Time(立ち上がり時間)の設定は必要なく、 fmax と dtN の設定を要する。本プログラムでは、中村・宮武関数における時刻歴関数を指定された時間刻み(= dtN)で作成し、そのフーリエ変換を震源スペクトルとして用いる。 そのため、 時間刻み(= dtN) が十分小さな関数を用いて震源スペクトルに用いる必要がある。 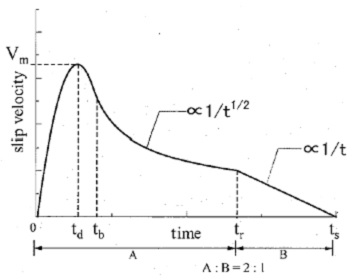 図1-1 中村-宮武(2000)によるすべり速度・加速度関数 (http://www.eri.u-tokyo.ac.jp/miyatake/SlipFunc-Prog.html) 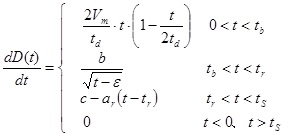 …(1-1) …(1-1)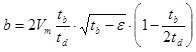 …(1-2) …(1-2)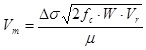 、 、 である。tbは図1-2に示すように、すべり速度が立ち上がりの2次関数からKostrov型関数に移行する時間であり、(1-1)式にすべり変位を与えることで自動的に決定される。さらに、CとarはKostrov型関数から振幅0に移行するまでを1次関数で補間するための係数である。 具体的なパラメータの値は、全断層面をアスペリティーとしてレシピ(2008)に準拠して設定する。 レシピでは破壊伝播速度(Vr)はVsの0.72倍としているが、ここではステップ2のT21モデルや、同時に実施している統計的グリーン関数法のベンチマークテストのモデルに整合させるため、3000 m/sとした。一方、実行応力Δσは、円形クラックの静的応力降下量(Eshelby 、1957)より算出する。 ここで、M0=μDLW≒1.03674×1018 (Nm)、μ=ρVs2≒3.2398×1010 (Pa)、D=1 mである。またRは断層面を円に置き換えたときの等価半径であり、R≒3191.5 mである。よって、Vmは と求まる。その他のパラメータは、中村-宮武(2000)によるフォートランコードを用いて、次の値を得る。 tb≒0.08284 s, c≒0.58094 m/s, ar≒1.7427 m/s/s, b≒0.45000 ε≒0.06667 これらの値によるすべり速度・加速度関数を図1-3に、そのフーリエ振幅スペクトルを図1-4に示す。Hisada(1991)などで議論されているように、すべり加速度関数のスペクトルはFmaxより低振動数ではほぼフラット、Fmaxより高振動数では1/ωのオーダーで減少する関数となっている。 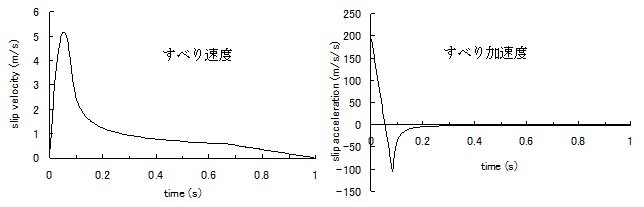 図1-3 すべり速度・加速度関数 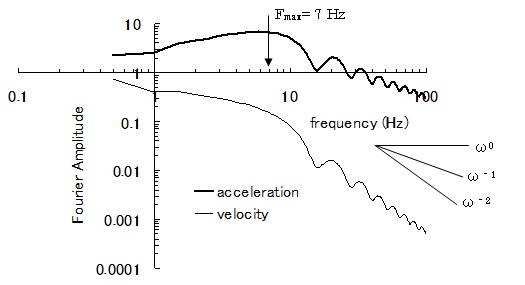 図1-4 すべり速度・加速度関数のフーリエ振幅スペクトル |
|||||||||||||||||
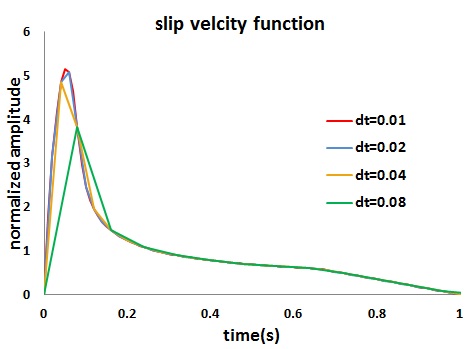 すべり速度関数(図1)
すべり速度関数(図1)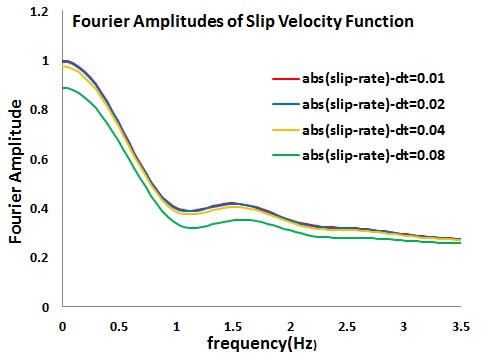 フーリエ振幅スペクトル(図2)
フーリエ振幅スペクトル(図2)