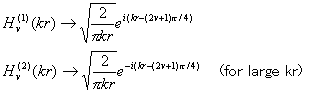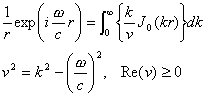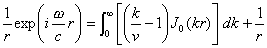The contour deformation method proposed by Greenfield (1995) is easy to formulate, but it is not effective for small horizontal distances. The asymptotic method that used is effective for both large and small distances, but it is not easy to formulate because of its mathematical complexity. Therefore, we make the source codes for our method (Hisasa, 1995) open to academic users through the anonymous FTP.
As mentioned in Greenfield (1995), we (Hisada, 1994) refined Apsel and Luco's asymptotic method (1983) to remedy the problem of slow convergence of the wavenumber integration of Green's function for layered half-space with source and receiver at same or close depths. Recently, we (Hisada, 1995) improved our method (Hisada, 1994) by deriving analytical asymptotic solutions including the reflected/transmitted waves from material boundaries, which are neglected in Hisada (1994). Independently, Zeng (1995) proposed a similar but numerical method.
An alternative method was proposed by Greenfield (1995), who uses a contour deformation for the integration path. We will examine the basic ideas of the two methods and check their merits and demerits. The integrands of Green's functions consist of the products of the displacement-stress vectors by the Bessel functions (see Hisada, 1994). Greenfield's method (1995) aims to make the Bessel functions converge. First, we transfer the Bessel functions to the Hankle functions, and second, we make use of their asymptotic solutions;

where h_v⁽ⁱ⁾ is the Hankle function of the order v, k is a wave-number and r is the horizontal distance between source and receiver. Finally, when we use the contour deformation for k, as shown in Figure 1 in Greenfield (1995), we could reduce the integration range because of the convergences of exp(-Imag(k)r) of h_v⁽¹⁾kr and h_v⁽²⁾kr for large kr.
The advantage of Greenfield's method is that it is easy to formulate without knowing any complicated mathematical properties of the displacement-stress vectors.
However, it is clear that this method is not effective for small r, because exp(-Imag(k)r) would converge slowly. In addition, we would need a careful check to find the best choice among several parameters: frequency, r, increments of Real(k) and Imag(k) for the numerical integrations, and the locations of C, D, and E in Figure 1 in Greenfield (1995).
On the contrary, our method aims to make the displacement-stress vectors converge and is effective for small and large r. To illustrate this, we show the simplest example used in Greenfield (1995) and Hisada (1994). The original wave-number integration is

where h and z are the depths of source and receiver, respectively, c is the velocity of the medium, and ƒÖ is the circular frequency. In this case, k/v corresponds to the displacement-stress vectors. In our method (Hisada, 1994), equation (2) can be

It is clear that the ( ) part in equation (3) converges with increasing k.
Figure 1 shows the comparisons of the integrands between equations (2) and (3) for the case of c=2000(m/sec), f=1(Hz), Q=100, and (a) r=2000(m) and (b) r=1(m). Only the real parts of the integrands are shown, because the imaginary parts quickly become zeros after passing the branch point (k=ƒÖ/c). Q is included to avoid the divergence at the branch point. In the Figure, the original integrands (equation (2), solid lines) slowly converge. In particular, the convergence for small r (=1) is extremely slow. In contrast, the integrands by our method (equation (3), dashed lines) quickly converge after passing the branch point even for small r.
In addition to this advantage, our method is numerically stable up to the infinite frequency and/or wavenumber, because we adopted the R/T matrix method, which does not have any exponential terms growing with wavenumbers. All those advantages are baneficial to the boundary element method (BEM) for a layered half-space (see Hisada et al., 1993), in which we require many Green's functions with small to large r.
One disadvantage of the method is that it is not easy to formulate for the case of layered half-spaces, because their displacement-stress vectors have complicated mathematical forms. To make ease of this, I made the FORTRAN codes for our method (Hisada, 1995) open to public users through the anonymous FTP. The address is "coda.usc.edu" or "128.125.23.15", the user name is "anonymous", and the directory is "pub/hisada/green".
In conclusion, Greenfield's method aims to make the Bessel functions (the Hankle functions) converge. It is easy to formulate, but its application is limited to a large r. Our method aims to make the displacement-stress vectors converge and is effective for small and large r. The combination of the two methods may give the fastest convergence.

1. Apsel, R.J. and J.E.Luco (1983). On the Green's functions for a layered half-space, part 2, Bull. Seism. soc. Am. 73, 931-951.
2. Greenfield, R.J. (1995). Comment on "An efficient method for computing Green's functions for a layered half-space with sources and receivers at close depths" by Y.Hisada, Bull. Seism. Soc. Am. 85, 1523-1524.
3. Hisada, Y. (1994). An efficient method for computing Green's function for a layered half-space with sources and receivers at close depths, Bull. Seism. Soc. Am. 93, 1700-1720.
4. Hisada, Y. (1995). An efficient method for computing Green's function for a layered half-space with sources and receivers at close depths (part 2), Bull. Seism. Soc. Am. (accepted).
5. Hisada, Y., K. Aki, and T.L. Teng (1993). 3-D simulations of surface wave propagation in the Kanto sedimentary basin, Japan (Part 2: application of the surface wave BEM), Bull. Seism. Soc. Am. 84, 1456-1472.
6. Zeng, Y. (1995). Synthetic seismogram computation in a layered elastic half-space with source and receiver located at close depth ranges, Geophys. J. Int. (submitted).