Bulletin of the Seismological Society of America, Vol. 83, No 6, pp. 1700-1720, December 1993

ABSTRACT

The 3-D surface wave Boundary Element Method is applied to the same set of strong motion records as those of Part 1 (Kato et al., 1993), namely, the long-period strong motion with periods around 8 sec recorded at the JMA (Japan Meteorological Agency) stations in Yokohama and Tokyo during the 1980 Izu-hanto-toho-oki earthquake. This method simulates exact Love and Rayleigh waves in a laterally heterogeneous medium including 3-D basin structures. The needed computer memory and CPU time are made manageable by assuming the inside and outside of the basin to consist of horizontal flat layers. In addition, vertical interfaces are assumed between the basin and the outside bedrock for simplicity in this study. After checking the range of validity of the flat-layer approximation for the Kanto sedimentary basin, the generation and propagation of surface waves in the basin are numerically investigated. In particular, our investigation places special emphasis on the cause of the observed long duration, which could not be explained in Part 1 using the surface wave Gaussian Beam method. When the bedrock outside the western margin of the Kanto basin is incorporated into the model, the observed long duration at the Tokyo station is successfully reproduced. This can be explained by the strong surface waves generated by the surface wave to surface wave conversion at the margin and appearing in Tokyo after the direct surface waves from the epicenter. This result agrees with Kinoshita et al.(1992), who studied records from an array of seismographs in Tokyo. Moreover, when a sedimentary basin of Sagami Bay is included as was done in Part 1, the simulations are greatly improved, particularly at the Yokohama station, which corresponds to the node in the radiation pattern of the source. This is due to the fact that the radiation pattern is strongly affected by the near-source heterogeneity of the Sagami basin. All these results, together with direct comparisons to 2-D modelings, clearly show the strong 3-D effects of the basin structures on the generation and propagation of surface waves for this earthquake.

INTRODUCTION

As shown in Kato et al.(1993), referred to as "Part 1" hereafter, the surface wave Gaussian Beam method successfully reproduced the long-period strong ground motions at the Yokohama and Tokyo stations during the 1980 Izu-hanto-toho-oki earthquake, except their long durations. The observational results (see e.g., Kinoshita et al., 1992, and the Introduction and Discussion of Part 1) have suggested that the long durations are caused by the secondary surface waves generated at the western margin of the Kanto basin. The presence of these surface waves arriving from directions other than the backazimuth to epicenter has been recently reported by several researchers based on 3-D numerical results (e.g., Toshinawa and Ohmachi, 1992; Frankel and Vidale, 1992). Because the surface wave Gaussian Beam method is effective only for a smoothly varying medium, we need to use a more accurate method to simulate these surface waves generated by a sharp medium boundary.
In this study, we employ a new 3-D Boundary Element Method (BEM) proposed by Hisada et al.(1991). BEM or Boundary Integral Equation Method (BIEM) is one of the most effective methods to simulate the exact wave field in a basin structure embedded in a half-space. They reduce greatly the number of discretized elements, and thus reduce numerical errors (e.g., the grid dispersion). In this regard, BEM compares favorably with other conventional methods, such as Finite Element Method and Finite Difference Method. Thus, we find their numerous applications to problems of wave propagation in basin structures (Wong et al., 1977; Sanchez-Sesma and Esquivel, 1979; Dravinski, 1982; Yamamoto et al., 1989; Kawase and Aki, 1989). However, usual BEM still has severe computational limitation when applied to 3-D problems, because we need to solve large full matrix equations, consisting of integrals of Green's function itself is usually time consuming, when we consider a layered half-space. Therefore, researchers have been using simple models, targeting relatively long-periods (e.g., Mossessian and Dravinski, 1990). In our new BEM, we assume flat-layered structures inside and outside a basin (see Fig.1) and extensively use the normal mode solution as the integral kernel. We also assume vertical interfaces between the basin and the outside bedrock. These assumptions greatly simplify our problems and make possible to simulate strong motions in actual large-scale sedimentary basins without heavy computations. Recently, similar but more approximate methods have been proposed by Fujiwara and Takenaka (1991) and Sanchez-Sesma et al.(1992), independently. Our assumptions are probably valid for long-period surface waves in shallow basins. On the other hand, Bostok (1991) proposed a T-matrix method for surface wave scattering from 3-D cylindrical obstacle.
In the following, we shall briefly summarize the formulation of our method, check the validity of the flat-layer approximation for the Kanto basin, and apply it to the target records mentioned earlier. In particular, we explore the cause of the observed long duration, which could not be simulated in Part 1 using the Gaussian Beam method.

THE FORMULATION OF THE SURFACE WAVE BEM

Because the BEM itself is well described in many text books (e.g., Kobayashi, 1987), we briefly summarize its formulation with some remarks important to our problem. We carry out all procedures shown below in the frequency domain, and then transform the results into the time domain using the FFT algorithm. Although we show here the case of two different layered-structures, the extension to three or more is straightforward, which is maybe required in the future's study.
Figure 1 shows the 3-D basin model considered. It consists of two flat-layered domains: one inside domain composed of sedimentary layers overlying crustal layers, and the other outside domain consisting only of crustal layers. First, we express wave fields in both domains by the representation theorem:

...............(1)

where, the superscripts I and O stand for the inside and outside domains, respectively, the subscripts designate vector and tensor components in a Cartesian coordinate system, and the summation convention is used. U_i(X) and P_i(X) are the displacement and traction at a point X; U_ik^*(X,Y) and P_ik^*(X,Y) are the fundamental solutions (integral kernels) of the layered half-spaces, ƒ¡ is the interface between both domains, C(Y) is a coefficient depending on the location of Y, and U_k^S(X_S,Y) is the incident wave from a seismic source located at X_S.
Second, we discretize the interface ƒ¡ along both vertical and horizontal directions from the free surface to a certain finite depth. Althouth we can consider any complicated shape for the interface, we assume it to be vertical and adopt the rectangular element having constant dispalcement and traction within each element. When we locate the point Y at the center of the pth element, the coefficient C(Y) is equal to 0.5, and the equation (1) is expressed as:

...............(2)

and,

...............(3)

where, ƒÂ_pq and ƒÂ_ik are Kronecker's delta functions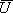, _i^q and 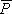_i^q are the constant displacement and traction on the qth element, M is the total number of the elements, and ƒ¢ƒ¡_q is the area of the qth element.
Third, taking the point Y on all elements, we obtain the following matrix forms from the equation (2):

...............(4)

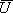where, {} and {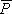} are the displacement and traction vectors of the boundary elements, {ĢU^*>} and {ĢP^*} are the coefficient matrices whose elements are obtained from the equation (3), [E] is the identity matrix, and {U^S} is the vector representing the incident wave.
Finally, imposing the continuity conditions for the displacement and traction at each element:

...............(5)

we obtain linear equations regarding the displacements and tractions along the interface.
In order to obtain the displacement at an arbitrary point Y inside or outside the basin, we substitute the boundary values {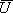} and {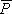} into the equation (1), and carry out the integration along the boundary using the same discretization technique shown above. For example, when a point Y is located on the free surface of the basin, the coefficient C(Y) equals 1 and the displacement at Y is obtained by

...............(6)

This process is much faster than that to obtain the boundary values, because it is not necessary to solve linear equations. However, this method is not probably economical to obtain "snapshots", because the large number of boundary integrations is repeatedly required, which equals the number of observation points to cover a wide region.
We employ both complete Green's functions of the layered half-spaces and the normal mode solutions as the fundamental solutions: U_ik^*(X,Y) and P_ik^*(X,Y), for the two domains. Because the calculation of complete Green's functions consumes a large amount of CPU time to carry out numerical integrations with respect to the horizontal wavenumber, it is desirable to use the normal mode solutions as much as possible. However, the linear equations become singular without complete Green's functions, because the normal mode solutions do not express the near diagonal terms of our coefficient matrices, which correspond to the case that an observation point X and a source point Y are located on a same vertical line. In this study, we introduce a critical distance from a source point Y to an observation point X, and choose complete Green's functions only within this distance. Because we chiefly use the normal mode solutions, we call our method "the surface wave BEM" in this study. We follow Harkrider (1964) for the formulation of Green's functions and the normal mode solutions. Because the formulation is based on the propagator matrix of Thomson and Haskell having growing exponential terms, this sometimes gives instabilities at higher frequencies.
This BEM drastically reduces the need for both computer memory and CPU time for seismic response problems of 2-D/3-D shallow basins as compared with conventional BEM, because, in addition to the fast computation of normal mode solution, the boundary elements are required neither for the basin bottom nor for the free surface. When we truncate the boundary elements at the certain depth in the underlying half-spaces, which should be deeper than the depth of the seismic source, this method assures good accuracy, because the amplitude of the normal mode solution decreases exponentially with depth and the downgoing body waves with usually small amplitude only exist in the underlying half-spaces. On the other hand, as well known in other exterior problems in acoustics and elastodynamics, this BEM probably suffers "the fictitious eigenfrequency problem"; unique solutions are lost at the certain frequencies corresponding to the eigenfrequencies of the interior region filled with the material properties of the exterior region (see e.g., Kobayashi, 1987). However, because the eigenfrequencies of the whole basin considered in this study are much smaller than the frequency window adopted, this problem would have no effects to our solutions. The description of this problem and its remedies are given by Kobayashi (1987). The validity of our method was demonstrated by Hisada (1992) who compared its result with those obtained by the conventional BEM based on Green's function of a homogeneous full-space.
Because the geology and the shear-wave velocity structure in and around the Kanto sedimentary basin are described in Part 1, we mention only additional information to construct appropriate flat-layered structures inside and outside the basin. Figure 2 illustrates the geological condition of the Kanto basin, together with the locations of the 1980 Izu-hanto-toho-oki earthquake, the observation stations in Tokyo and Yokohama, and three deep bore-hole stations: Fuchu, Iwatsuki, and Shimosa. Note that Sagami Bay containing soft sediments is located between the earthquake epicenter and the observation stations. Figure 3 shows shear-wave velocity profiles directly measured at the three bore-holes (Yamamizu et al., 1981), together with the Kinoshita's estimation in Tokyo (Kinoshita et al., 1992). From these profiles, we can see very similar velocity structures at all locations. This allows us to justify the flat-layer approximation within the basin, at least from its center to the western margin of the of the basin. On the other hand, the bedrocks outside the western and southern margins are considerably different; volcanic and Pre-Tertiary rocks outside the western margin, and Tertiary rocks outside the southern margin. We, thus, will use two different flat-layered bedrock structures: the crustal layer structure based on the results by Yamanaka (1990) for the western bedrocks, and that based onthe results by the Research Group on the Underground Structure in Tokyo (1989) for the southern bedrocks. We use the results by Kakimi (1973) to construct the boundary between the Kanto basin and the surrounding bedrocks, as shown in Figure 2.
On the basis of the above information, we adopt the following four 3-D Kanto basin models and two 2-D models, as shown in Figures 4a to 4e and 5. The first model (3-D model 1) consists of a Quaternary sedimentary basin (V_s of its top layer = 1.3 km/sec). Its plan and cross section are shown in Figures 4a and 5a, respectively. In these figures, the bold solid lines indicate the BEM mesh area. Thirty-six elements along the horizontal and four elements along the vertical directions are used in this modeling. The total number of boundary elements is thus 144 (=36*4). Note that we neglact the northern margin of the basin, because the reflected waves from this margin will arrive late enough to be negligible in the main motions observed at the Tokyo and Yokohama station. Although we terminate the horizontal element at the locations shown in Figure 4a, and also in the subsequent models in Figures 4b to 4e, we have confirmed that the coice of the location of terminal element has little effects on the simulation results at the Tokyo and Yokohama stations for the target earthquake.
Figure 4b and Figure 5b show the plan and cross section of the second model (3-D model 2), respectively. In this case, the Quaternary sedimentary basin is in contact with the hard Pre-Tertiary bedrock (V_s of its top layer = 2.5 km/sec). In addition to the northern margin of the basin, the eastern margin is also neglacted in this modeling, because there is no clear boundary between the Quaternary basin and the Pre-Tertiary bedrocks along this margin, as seen in Figure 2. The number of total boundary elements is 108(=27*4) for this case.
The third and fourth model (3-D model 3 and 4) are almost identical to 3-D model 1 and 2, respectively, except the presence of the low-velocity Sagami basin adfacent to the Kanto basin (Figs. 4c and 4d). The layered structure in the Sagami basin is assumed to be identical to that of the Kanto basin, bacause of the lack of information for the structure and of the limitation of our method. As demonstrated in Part 1, the Sagami basin would have strong effects on the surface wave propagation in the Kanto basin for the target earthquake. The numbers of boundary elements in both models are 180(=45*4).
Finally, we use two 2-D basin models corresponding to 3-D models 1 and 2, respectively, to check the validity of 2-D approximation (Fig.4e). Note that although the structures are 2-D, the source is 3-D and identical to those used in 3-D models. The number of boundary elements is 72(=18*4) in this case.

RESULTS

Table 1 shows the source parameters used in this study. The results of Part 1 and also our preliminary simulations (partly in Aki et al., 1992) have shown that the excitation of the surface waves at the source and the edge of the basin is very sensitive to some source parameters, particularly the depth and strike (radiation pattern). Since the final source parameters used in Part 1 ("Model B") gave an excellent agreement with the observations, the parameters adopted here are nearly the same as those used in Part 1, which is originally derived from the Takeo's inversion results (Takeo, 1988).
Figures 6a and 6b are the observed records at the JMA stations in Yokohama and Tokyo during this earthquake, respectively. These and all subsequent synthetic displacements are bandpass filtered between periods of 6.28 sec and 10.5 sec by a trapezoidal filter with flat range from 6.98 sec to 8.98 sec. Times in Figure 6 and all subsequent displacements are measured from the origin time of the earthquake.
We use the critical distance of 20km in the following computations, which is difined above in "The formulation of the surface wave BEM". We assume frequency independent Q-values 50, 100, and 150 in the basin, Tertiary Pre-Tertiary bedrocks, respectively, for the normal mode solution. We have checked the accuracy of our method by comparing results with analytical solutions computed by complete Green's function for several flat-layered models. The computing time required for our simulation varies between 15 and 30 hours of CPU time on a Sun 4/490 workstation, depending on the specific case being studied.

TABLE 1: The fault geometry and the kinematic source parameters of the 1980 Izu-hanto-toho-oki earthquake

Location of Source		Depth (km)		Strike Direction		Dip Direction		Dip Angle		Rake Angle
(N34.9',E139.2')		5.0		N10.0'W		N80.0'E		84.0'		16.0'

Length (km)		Width (km)		Dislocation (m)		Rise time (sec)		Rupture velocity (km/sec)
20.0		10.0		1.16		1.0		2.0

Moment (dyne* cm)		Rupture type
7.0*1025		bilateral

3-D Model 1(Tertiary Bedrock Model) and 2(Pre-Tertiary Bedrock Model)
Solid lines in Figures 7a and 7b are displacements computed at the Yokohama station using 3-D models 1 and 2, respectively. We also plot results obtained by corresponding 2-D models by dotted lines in the same figures. The effects of the western edge are negligible and the 2-D models seem to be appropriate in these cases, because we cannot distinguish large differences between the 3-D and 2-D models. However, we find some discrepancies between them and the observed record shown in Figure 6a. The simulated motions arrive earlier and their durations are somewhat shorter than the observation, particularly for 3-D model 2. This is probably due to the fact that we neglect the low velocity basin in Sagami Bay. In addition, they are small in amplitude, particularly for E-W components, because the Yokohama station corresponds to the node of the radiation pattern of Love waves of our source model, as discussed in Part 1.
Figures 8a and 8b are simulated displacements at the Tokyo station using the same models. In this case, although the first arrivals are in a good agreement between the 3-D and 2-D models, we see large differences in later arrivals. The 3-D models generate strong later arrivals, and thus substantially prolong their durations. They are very similar in both wave form and duration with the observed (Fig.6b). Mafor differences lie in the smaller E-W components than in the N-S components in the simulated motion. As shown below, this is because the N-S components nearly correspond to the particle directions of the Love waves, which come from the western margin. As seen in the small vertical amplitudes, Love waves are dominant over Rayleigh waves.
We now examine where the later arrivals at the Tokyo station are generated and in which direction they propagate. Because we have obtained almost the same conclusions among all components for the two 3-D models, we will show only results of the N-S component for the 3-D model 2. We compute displacements along several lines centered at the Tokyo station at intervals of 5km. Figures 9a and 9b show the results along the line N120E and N30E, respectively. As seen in Figure 4b, the line N30E corresponds to the line from the source to the Tokyo station, and the line N120E is perpendicular to the line N30E. From Figure 9a, the first couple of cycles at the Tokyo station are interpreted as direct arrivals from the source, because they are in phase with each other along the line N120E. However, the later arrivals clearly come from directions departing from the direction to epicenter. Similarly, Figures 10a and 10b show displacements of N-S components computed along the line N140E and N50E, respectively (see their locations in Fig.4b). The later arrivals in this case are in phase with each other along the line N140E. Therefore, they propagate along the line N50E perpendicular to the N140E. As found in Figure 10b, they are generated at the western margin of the Kanto basin and propagate toward Tokyo with low phase velocities (1.7 to 2.1 km/sec). Because the fundamental Love mode is dominant in the basin within the frequency window considered, the later arrivals are interpreted mainly as the Love waves of fundamental mode converted from the surface waves propagating in the bedrock along the western margin. These results agree with the observational results by Kinoshita et al.(1992), who obtained N55E and 1.9 to 2.4 km/sec for the direction of propagation and the phase velocities of the Love wave of the fundamental mode, respectively.

3-D Models 3 and 4(3-D Models 1 and 2, Respectively, Plus the Sagami Basin)
Figures 11a and 11b represent simulated displacements at the Yokohama station using 3-D models 3 and 4, respectively. Similarly, Figures 12a and 12b are those at the Tokyo station. Compared with the results of 3-D models 1 and 2, the inclusion of the Sagami basin clearly improves our simulations, particularly at the Yokohama station. However, 3-D model 3 overstimates the amplitude of the observed motions (note the different amplitude scale in this case). This is probably because the low velocity structure in the Sagami basin focuses too strongly the surface wave energy toward the direction of the two stations in this model. In both cases, the surface wave energy is trapped within the Sagami basin, reflected between basin edges, because of the strong impedance contrast between the bedrock and the basin, and slowly radiated from the basin. Consequently, we obtain the simulated motions with considerably long durations.
An important conclusion reached here is that the inclusion of low-velocity Sagami basin in the model substantially changes our simulation results. We can reproduce the observed large amplitude with this low-velocity basin located near the earthquake, even though the observation stations correspond to the nodal plane of the radiation pattern of our source model. This is undoubtebly indispensable to simulate the strong motion at Yokohama station for this earthquake, as demonstrated here and also in Part 1. As shown in this study, we can also simulate the observed long duration using Sagami basin models with the strong impedance contrasts between the bedrock and the basin, which may be unrealistic. For further investigations, we need more accurate information on this structure and also more rigorous methods that may require greater computer memory and/or CPU time.

CONCLUSIONS

We have investigated seismic motions in the Kanto basin with periods of 6 to 10 sec due to the 1980 Izu-hanto-toho-oki earthquake. In order to simulate the secondary surface waves generated at the basin edges, we have used the 3-D surface wave BEM. Comparing the observed records with those simulated for several models, we have obtained quantitative understanding of the cause of the observed long duration and also large amplitude at the Tokyo and Yokohama stations. When we model the western margin of the Kanto basin by a vertical discontinuity, strong surface waves are generated by the surface wave to surface wave conversion at the margin and arrive at the Tokyo station after the direct surface waves from the source direction. The long duration of the records observed at the Tokyo station is, thus, successfully reproduces. The calculated arrival direction and phase velocities of the secondary surface waves agree with the observational results by Kinoshita et al.(1992(. On the other hand, when we include the low-velocity Sagami sedimentary basin, the simulations are greatly improved at the Yokohama station, which corresponds to the node of the radiation pattern of the source. The large amplitude is caused by the fact that the Sagami basin located near the epicenter substantially distorts and obscures the radiation pattern. This conclusion is in agreement with that obtained in Part 1 (Kato et al., 1993). The longer duration is also simulated using the Sagami basin models with strong impedance contrasts between the basin and the surrounding bedrock, because the surface wave energy are trapped within the basin, reflected between basin edges, and slowly radiated from the basin.
To summarize the combined efforts of Parts 1 and 2, we first have confirmed that the surface wave Gaussian beam method is a powerful and economical tool to simulate the early part of the surface waves in a basin structure, as far as the assumption of a smoothly varying medium is valid. When sharp velocity contrasts exist around the basin edge, like the western margin of the Kanto basin, the surface wave BEM is appropriate to take into account the secondary surface waves generated along the edge, which substantially lengthen the duration of the strong motion in the basin. Second, we have found that the long-period strong motion in the basin is very sensitive to not only the source depth and the radiation pattern, but also to the whole 3-D structures of the Kanto and Sagami basins. Basins such as Kanto and Los Angeles, where the largest global metropolitan developments will undoubtedly continue to take place, deserve this type of long-period strong motion studies.

ACKNOWLEDGMENTS

This work was partly supported by the Kajima-CUREe project. We would like to thank Drs. M.Niwa, M.Takemura, M.Motosaka, H.Yamanaka and Mr. M.Kamata and K.Urao of the Kajima Corporation for inspiring and informative interactions throughout the period of this project. They kindly provided us the digital strong motion data at the Tokyo and Yokohama stations. We are also grateful to K.Kato and X.F.Chen for valuable discussions. The original manuscript was greatly improved by the comments of J.Vidale and anonymous reviewers. This work was also supported in part by the National Science Foundation under the grant BCS-9024487.