ć8ńú{nkHwV|WE 1990
AMPLIFICATION FACTOR DUE TO LOVE WAVES IN MULTI-LAYERED SEDIMENTARY BASINS
by Yoshiaki Hisada*, Shunroku Yamamoto** and Sukenobu Tani***
* Yoshiaki Hisada: Research Assistant, School of Science and Engineering, Waseda University
** Shunroku Yamamoto: Graduate Student, School of Science and Engineering, Waseda University
*** Sukenobu Tani: Professor, School of Science and Engineering, Waseda University
- ABSTRACT
-
Amplification factors due to Love waves generated in multi-layered sedimentary basins are investigated for incident plane SH-waves, horizontally propagating in a homogeneous half-space bedrock. The factors are analytically computed considering the basin models composed of horizontally flat-layers having a vertical lateral boundary with the bedrock. These factors are found to be sharply peaked at frequencies corresponding to the Airy phases when impedance ratios between adjacent layers including bottom bedrock are large. As the impedance ratios become small, the peaks smoothen. The spectral shape of the amplification factors is similar to that due to the body SH-waves, with smaller amplitude, in particular for higher modes.
- INTRODUCTION
-
To investigate the site effect in a class of sedimentary basins and alluvial valleys where the width is much larger than the thickness, we need to study the amplification factor including two kind of waves; body waves amplified in the sediments and surface waves locally generated in the basins 1). The case of the amplification factor due to body waves in single layer overlying half-space has been investigated by Sezawa 2), and the extension to multi-layered media by Haskell 3). On the contrary the local surface waves are relatively a new topic and their effect on the basin response has been reported since early 1970 using numerical modeling 4) and field measurements 5),6),7),8), In particular it has become an important subject to explain the long duration strong motion records observed in Mexico City during the 1985 Michoacan earthquake 9).
In this paper we investigate amplification factors due to Love waves generated in multi-layered sedimentary basins. We consider incident plane SH-waves horizontally propagating in a homogeneous half-space bedrock, for optimal generation of Love waves in the basin 1),10). We assume the basin models as composed of horizontally flat-layers having a vertical lateral boundary with the bedrock (see Fig.1), and compute the amplification factor due to Love waves generated at the vertical boundary using the analytic solution by Hisada et al.11). For the case of incident Love waves, Alsop 12) proposed an approximate method using a variational method. For the case of incident body SH-waves, on the other hand, we obtain directly an analytical solution using the representation theorem and the normal normal mode solution of the Love waves 11). In this study we particularly pay attention to the spectral shape of the amplification factor. It is well known that in the case of the body SH-wave this factor has sharp peaks at the predominant periods of layered structures with large impedance ratios between adjacent layers including the basement rock. On the contrary these sharp peaks do not exist when the impedance ratios are small 13). As examples of the former we can cite the Kanto basin (the Tokyo area, Japan) and the Mexico City valley. The latter corresponds to the El Centro area 14).
- AMPLIFICATION FACTOR DUE TO LOVE WAVES EXCITED AT A VERTICAL DISCONTINUITYK
-
Referring to Fig.1, the medium is composed of two 2-D elastic quarter-spaces welded along the vertical interface X=X', one quarter-space is homogeneous (Domain 1) and the other is layered with flat interfaces (Domain 2). Each layer is homogeneous. The incident wave is a plane SH-wave with unit amplitude, propagating horizontally in Domain 1. The reflected wave from the vertical interface is also a plane SH-wave with constant amplitude, assuming that we can neglect the contribution of the waves diffracted at the corners formed by each layer and the vertical interface. The waves transmitted into Domain 2 are the superposition of Love wave modes (normal modes). Assuming the time-dependent factor as eiÖt, the analytic expression of the Love wave V2 at Ě1 on the free surface in Domain 2 is given as follows 11);
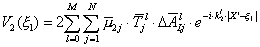 ...............(1)
...............(1)
where M is the maximum Love mode for the considered frequency Ö, N is the total number of layers including the bottom bedrock, 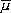 2j is the rigidity of the jth layer, and k2l is the wave number of lth Love mode, The transmission coefficient
2j is the rigidity of the jth layer, and k2l is the wave number of lth Love mode, The transmission coefficient 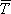 jl is
jl is
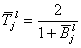 ...............(2)
...............(2)
where 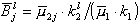 , Ę1 is the rigidity of Domain 1 and k1 is the wave number of the incident wave.
, Ę1 is the rigidity of Domain 1 and k1 is the wave number of the incident wave.
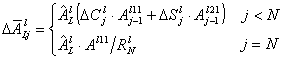 ...............(3)
...............(3)
where ˘Cjl, ˘Sjl, ˘RNl are respectively
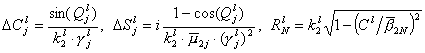 ...............(4)
...............(4)
Cl being the phase velocity of lth Love mode. The detail of the medium response 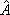 Ll, elements of the Haskell's propagator matrix
Ll, elements of the Haskell's propagator matrix 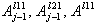 , and functions Qjl and Ájl are given in the references 11),15).
, and functions Qjl and Ájl are given in the references 11),15).
Finally the amplification factor AFLl on the free surface due to lth Love mode is derived from the absolute value of lth mode of equation (1), as follows;
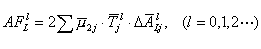 ...............(5)
...............(5)
Note that this value is independent of the distance from the vertical boundary (the basin edge).
- AMPLIFICATION FACTOR DUE TO LOVE WAVES IN MULTI-LAYERED SEDIMENTARY BASIN
-
We compute amplification factor due to Love waves excited in four basin models with the layer structure illustrated in Fig.2. The depth of the interface of the basin with the bottom bedrock is 2km in all of them, but the number of layers varies for each model from one to eight. The material properties of the layers (VS, Ď) increase with depth and we assign the values VS=0.5km/s, Ď=1.8t/m3 to the top layer and VS=2.5km/s, Ď=2.5t/m3 to the bedrock in all models.
Fig.3 shows dispersion curves of Love waves for each model. Solid lines indicate phase velocities and dotted lines group velocities. For models with fewer layers and large impedance ratios between adjacent layers including bedrock, values of the both velocities sharply vary from maximum (2.5km/s) to minimum (under 0.5km/s) around frequencies corresponding to the Airy phases as marked with triangles in the figure. On the contrary, for models with many layers and small impedance ratios, values of both velocities gradually vary, and we can not see clearly the Airy phase.
Fig.4 shows amplification factors due to Love waves inside the basin (solid lines) and to the vertical incidence of body SH-waves upon the layered structure without the vertical boundary (dotted lines). For this we have used the Haskell's method 3). The factor due to Love waves has similar spectral shape to that due to body waves, but smaller amplitude. For models with fewer layers, both factors are sharply peaked at the frequencies corresponding to the Airy phases. On the contrary, for models with larger number of layers, the spectral shape of the factors flattens, decreasing the values of the peaks and increasing the values of the troughs. The amplification factors due to Love waves show the largest peak-values for the fundamental mode in all models, according to the fact that particle motion of an horizontally incident plane-wave is in phase with that of the fundamental mode. For higher modes the particle motion is 1 out of phase at certain depth.
- CONCLUSIONS
-
In this paper we have used an analytical solution of Love waves generated in a complex sedimentary basin to study the amplification effects of these waves in the basin, upon the incidence of horizontally propagating plane SH-waves. Our analytical solution is suited for this problem because it represents accurately the Love waves, although it neglects the body wave contribution 11). The amplification effects are studied by computing the amplification factor at the free surface of the basin. We found that when impedance ratios between adjacent layers including bottom bedrock are large, such as the Tokyo area 14), the amplification factors are sharply peaked at frequencies corresponding to the Airy phases. On the contrary when the ratios are small, such as the El Centro area, the spectral shape of the amplification factors becomes more smooth, decreasing the values of the peaks and increasing the values of troughs. Additionally, we have computed the amplification factors due to body SH-waves for vertically incidence using the Haskell's method, for comparison. We found that both spectral shapes are similar, although the one corresponding to the Love wave is of smaller amplitude, in particular for higher modes. This is because the particle motion of the higher modes at certan depth is out off phase with that of an horizontally incident plane-wave, which is constant along the whole depth.
- ACKNOWLEDGMENTS
-
We are grateful to R.Benites for many fruitful discussions and help to improve the manuscript, and to K.Aki for many helpful suggestions. Part of this work was done while one of the authors (Y.H.) was a visiting scholar at the Department of Geological Sciences, University of Southern California.
REFFERENCES
- Bard, P.-Y. and M.Bouchon (1980). Bull. Seism. Soc. Am. 70, 1263-1286.
- Sezawa, K. (1930). Bull. Earthq. Res. Inst 8, 59-70.
- Haskell, N.A. (1960). J.Geophys. Res. 65, 4147-4150.
- Aki, K. and K.L.Larner (1970). J.Geophys. Res. 75, 933-954.
- Hanks, T.C. (1975). Bull. Seism. Soc. Am. 65, 193-225.
- Tanaka, T.S., S.Yoshizawa and Y.Osawa (1980). Proc. of the 7th World Conf. on Earthquake Engineering, vol.2, 609-616.
- Seo, K. and H.Kobayashi (1980). Proc. of the 7th World Conf. on Earthquake Engineering, part.1, 9-16.
- Toriumi, T., S.Ohba and N.Murai (1984). Proc. of the 8th World Conf. on Earthquake Engineering, vol.2, 465-472.
- Kawase, H. and K.Aki (1989). Bull. Seism. Soc. Am. 79, 1361-1382.
- Hisada, Y., S.Yamamoto and S.Tani (1988). Proc. of the 9th World Conf. on Earthquake Engineering, vol.2, 701-706.
- Hisada, Y., S.Yamamoto and S.Tani (1990). (submitted to Bull. Seism. Soc. Am.).
- Alsop, L.E. (1966). J.Geophys. Res. 71, 3969-3984.
- Kanai, K. (1957). Bull. Earthq. Res. Inst 35, 457-471.
- Seo, K., H.Yamanaka, T.Samano and S.Midorikawa (1988). Proc. of the 9th World Conf. on Earthquake Engineering, vol.2, 399-404.
- Harkrider, D.G. (1964). Bull. Seism. Soc. Am. 54, 627-679.
...............(1)
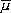 2j is the rigidity of the jth layer, and k2l is the wave number of lth Love mode, The transmission coefficient
2j is the rigidity of the jth layer, and k2l is the wave number of lth Love mode, The transmission coefficient 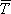 jl is
jl is...............(2)
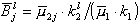 , Ę1 is the rigidity of Domain 1 and k1 is the wave number of the incident wave.
, Ę1 is the rigidity of Domain 1 and k1 is the wave number of the incident wave................(3)
...............(4)
 Ll, elements of the Haskell's propagator matrix
Ll, elements of the Haskell's propagator matrix  , and functions Qjl and Ájl are given in the references 11),15).
, and functions Qjl and Ájl are given in the references 11),15)................(5)